忧愁河上的金桥
介绍
一首暖心的经典歌曲,和这段程序最配了。为什么在阳光、黑暗和金桥之间设定这样的函数,只有自己最懂。
Song: Bridge Over Troubled Water
代码
Sunshine <- function(x) {
# Sunshine 为此函数名称,X 为函数中涉及到的参数
# 给出一个范围 1 到 20,而 s 取 20 中的任何一个
s <- sample(1:20,1)
# 用 x 进行一系列计算
m <- (x/5+3)*6-x*5+x^sqrt(1/3)
if (m > s)
# 如果计算结果大于 S,则输出“你得到了阳光!”
"your get sunshine !"
else if (m < s)
# 如果计算结果小于 S,则输出“你陷入了黑暗!”
"your fall into the dark !"
else
"your get the bridge!"
}
# 如果计算在s的范围内,则显示“你得到了一座桥”
演示
Sunshine(4)
## [1] "your fall into the dark !"
Sunshine(0)
## [1] "your get sunshine !"
点评
这也是一个猜数游戏,不过这个和之前的都有所不同。
首先调用 sample() 函数从 1 到 20 中随机选择一个整数,接着对用户猜的数进行计算后与随机数比较得到猜数游戏的结果。
不过由于输入参数再经过公式计算之后正好是整数,而且是 1 到 20 之间的整数的可能性很小,所以得到 bridge 还是非常难呢。
最后,还是想看一看那个处理输入数值的公式 (x/5+3)*6-x*5+x^sqrt(1/3)。我想问作者是怎么弄出这么个公式的呢,加减乘除和乘方(^)开方(sqrt())都给用上了。我们还是用 R 来看看这个函数的图形吧。
plot(function(x){(x/5+3)*6-x*5+x^sqrt(1/3)}, 0, 10, ylab = "func")
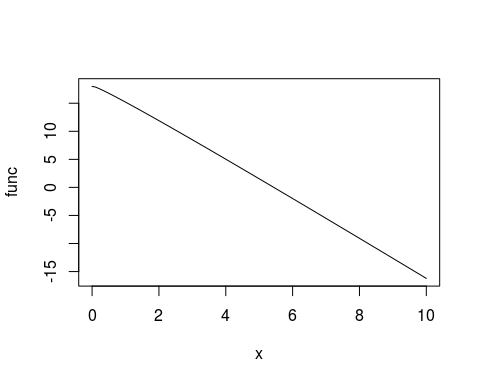
看这图形大体近似一条直线,最大值在 18 左右,零点在 5 到 6 之间,看来想得到阳光也不是那么容易呢。大家如果有兴趣还可以继续研究,找一下得到阳光的概率什么的,也会是个有意思的话题呢。